Metodologia fuzzy per l'analisi dei tessuti insediativi

Michele Grimaldi

Analizzando le città dal punto di vista della loro morfogenesi ci si accorge che lo spazio urbano si è enormemente dilatato, frammentato, disperso. Dalla città storica compatta si è passati, negli anni, a insediamenti sempre più ramificati e dispersi sul territorio, andandosi così a delineare un modello di città che viene definito: città diffusa.

Non a caso il fenomeno riscontrato con maggiore frequenza nell’analisi delle trasformazioni territoriali è quello della dispersione insediativa, denominata sprawl, periurbanizzazone, esplosione urbana, sub-urbanizzazione, le cui manifestazioni sono: “bassa densità, frammentazione territoriale, crescita incontrollata dell’urbano, dinamiche insediative a macchia d’olio, una pianificazione debole che accompagna e supporta processi di insediamento, talvolta ai margini della legalità” (Fregolent L., 2005).

Tutto questo si traduce, dal punto di vista del sistema insediativo, nel fatto che non assistiamo più alla dicotomia urbano-rurale, bensì ad una ambiguità tra questi due ambiti territoriali che può essere letta attraverso nuovi fenomeni insediativi.

Questa condizione ha portata mondiale, basta pensare allo sprawl di Chicago, vale a dire quel massiccio fenomeno di espansione e dispersione urbana che ha investito negli ultimi tre decenni l’area metropolitana di Chicago e che ha causato di conseguenza una drastica diminuzione delle aree naturali e del terreno agricolo, oppure al desakota phenomenon, tipico fenomeno di quelle regioni della Cina la cui urbanizzazione è contraddistinta dalla ambiguità urbano-rurale. Basta, infine, semplicemente guardarsi intorno.

“Mentre molto è stato fatto da geografi, urbanisti, sociologi per comprendere e documentare questo fenomeno, meno è stato fatto per quanto riguarda la misurazione sistematica della periurbanizzazione” (Heikkila E. D., Shen T., Yang K, 2001). Le principali ragioni di questa manchevolezza possono essere individuate nella complessità del fenomeno da analizzare e nella molteplicità di contesti territoriali in cui esso si manifesta.

L’obiettivo dello studio è quello di analizzare il tessuto insediativo sulla base di opportuni indicatori quantitativi, sfruttando le potenzialità dei sistemi inferenziali fuzzy per gestire qualitativamente la loro variabilità territoriale all’interno della regione di studio.

Richiami teorici

La logica fuzzy, formalizzata negli anni ’60 da Lotfi A. Zadeh, si colloca nell’ambito dell’intelligenza artificiale. Essa si pone come obiettivo di risolvere problemi, anche complessi, mediante regole empiriche e qualitative che interessano un mondo di azioni e di oggetti grigi e sfumati e non bianchi o neri dai contorni netti (logica tradizionale). Gli esseri umani si comportano come sofisticati sistemi di controllo o di decisione senza per questo essere matematici o risolutori di equazioni. Ad esempio, per decidere quando e quanto annaffiare un giardino sono sufficienti inferenze qualitative del tipo: la temperatura è alta e il suolo asciutto, allora il tempo di annaffiatura dovrà essere lungo. Il ricorso a inferenze qualitative si rivela utile per progettare sistemi di controllo o di supporto decisionale quando il relativo sistema matematico è ignoto o troppo complicato, oppure quando la soluzione di un problema è facilitata se si esclude la ricerca di precisione matematica.

I sistemi fuzzy o sistemi inferenziali fuzzy, indicati con la sigla Fis, che sta per fuzzy inference sistems, sono sistemi in grado di combinare concetti fuzzy, quali gli insiemi, le variabili linguistiche e la logica fuzzy, per produrre uscite crisp da un qualche input.

Un sistema fuzzy, come qualsiasi altro sistema classico, riceve in ingresso n variabili, e restituisce in uscita m grandezze. Nella teoria classica dei sistemi si dice che si conosce il modello matematico di un sistema quando si dispone di una o più equazioni che descrivono le relazioni fra le variabili di ingresso e quelle di uscita. Il problema che sorge è che spesso la modellizzazione matematica di un sistema risulta molto complessa, se non addirittura impossibile a meno di forti approssimazioni, a causa dell’elevato numero di variabili e della frequente non linearità. I sistemi fuzzy, basati sulla logica sfumata, si propongono come metodo completamente innovativo nell’affrontare problemi di questo tipo. Infatti, il sistema di equazioni è sostituito da una famiglia di regole logiche del tipo if-then che creano una corrispondenza tra insiemi fuzzy appartenenti a spazi diversi dando una descrizione linguistica del sistema. Questo approccio è in generale più semplice di quello classico e si presta particolarmente nel caso di problemi fortemente non lineari in cui l’intuizione e l’esperienza umana rivestono un ruolo fondamentale.

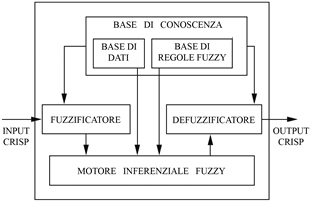
Il funzionamento si compone di tre fasi:

1. fuzzificazione;

2. inferenza;

3. defuzzificazione (Figura 1).

La fuzzificazione è quel processo che determina un valore rappresentante il grado di appartenenza di un determinato input ad ognuno dei fuzzy set definiti.

L’aspetto fondamentale nel processo è la scelta delle funzioni di appartenenza, che dipende, in generale, dal progettista del sistema sulla base della sua intuizione ed esperienza. Inizialmente si adoperavano funzione a campana (gaussiane), attualmente si preferisce usare combinazioni di funzioni di tipo L, G, P e L, che danno risultati molto simili e permettono una semplificazione dei calcoli. Indipendentemente dalla forma è importante che l’unione dei supporti degli insiemi della partizione ricopra tutto l’universo del discorso. Questo per evitare che ci siano valori di ingresso per i quali non sia possibile definire alcuna regola.

Il secondo passo è quello dell’inferenza. In tale modulo sono contenute le regole di composizione dei fuzzy set del passo precedente e, sulla base dei valori di membership degli insiemi sfumati, viene calcolato per ogni regola il valore di verità finale. Anche per tale passo la definizione delle opportune regole di composizione è lasciata a considerazioni euristiche spesso tratte dall’esperienza di esperti umani (composizione di conoscenze qualitative e quantitative).

Per definire in che modo il sistema derivi dalle azioni di controllo a partire da una base di regole è necessario definire: la funzione di implicazione, come vengono implementati i connettivi and e or (il primo usato nella definizione degli antecedenti e il secondo per combinare le azioni delle singole regole), e l’operatore di composizione (gli operatori di composizione più usati sono max-min e max-dot).

L’operazione di defuzzificazione consente di convertire un’azione di controllo generata dall’unità di inferenza sotto forma di un fuzzy set in una azione di controllo crisp, ossia un numero che rappresenti nel miglior modo possibile il fuzzy set in questione. Non esiste un criterio universalmente accettato che stabilisca come determinare questo valore. Esistono diverse strategie di defuzzificazione che si differenziano per la qualità dei risultati ottenuti e per la complessità dei calcoli necessari. Tra le più comuni si ritrovano il metodo del massimo, che produce il punto nel quale la funzione di appartenenza raggiunge il suo valore massimo, il metodo della media dei massimi, che restituisce il valore medio, nel caso in cui ci siano più punti in cui la funzione di appartenenza assume il valore massimo e il metodo del centroide, uno dei metodi più usati pur risultando oneroso dal punto di vista computazionale, che restituisce l’azione di output corrispondente al centro di massa della funzione di appartenenza.

Schema metodologico

L’analisi dei tessuti insediativi si propone la formalizzazione di un modello interpretativo delle diverse forme di insediamento che si manifestano su di un territorio antropizzato.

Premessa al nostro studio è che nel sistema insediativo possono essere individuate cinque forme di insediamento:

1. ambito urbano;

2. ambito periurbano ad alta densità;

3. ambito periurbano a bassa densità;

4. ambito metaurbano;

5. ambito extraurbano.

L’ambito urbano, è quella forma insediativa nella quale è riconoscibile una stretta complementarietà tra impianto viario e trama edilizia, consistente in una sostanziale giustapposizione ordinata fra trama viaria, isolati e lotti, e spesso caratterizzata dal parallelismo tra gli assi di giacitura dei corpi edilizi.

L’ambito periurbano è invece la fase periferica dei tessuti urbani consolidati che si protrae verso il tessuto rurale. Esso può essere contraddistinto da un’alta densità insediativa o da una bassa.

L’ambito metaurbano è invece quella forma insediativa caratterizzata dalla non complementarietà tra impianto viario e trama edilizia, posta al di là dell’ambito urbano e contraddistinta da una bassa densità.

L’ambito extraurbano coincide con il tessuto rurale ed è caratterizzato da insediamenti radi e sparsi e da una sostanziale integrità del paesaggio.

L’obiettivo dello studio è quello di giungere alla definizione di questi ultimi sulla base di opportuni indicatori.

Lo schema metodologico si compone di una prima fase, in cui si provvede alla determinazione degli indicatori, e di una seconda fase, in cui viene formalizzata la procedura che si fonda sul funzionamento di un sistema inferenziale fuzzy che processa in serie le n unità territoriali in cui è stata suddivisa l’area di studio restituendo la rappresentazione dei diversi ambiti territoriali.

Con riferimento alla prima fase, al fine di stabilire gli indicatori più significativi si è riflettuto sui principi e sui concetti in base ai quali identificare le aree urbanizzate del territorio. Essi non sono univoci. A tal proposito, abbiamo considerato le definizioni che l’Istat dà per quanto concerne il centro abitato, il nucleo abitato, la casa sparsa, i nuclei speciali. Esse si rifanno a parametri geometrici che consentono di valutare la contiguità degli edifici, ad un riscontro sulla presenza di servizi, esercizi pubblici, luoghi di raccolta, e anche a concetti più vaghi come i principi di socialità.

Ne è scaturita la scelta di considerare la densità edificatoria, espressa in termini di superficie coperta e di volumetria, e la presenza di attrattori e di reti come linee guida per la definizione di detti indicatori.

Si considera una regione ripartita in n unità territoriali non sovrapposte, ottenute sovrapponendo idealmente al territorio in esame una griglia a maglie quadre di cui va fissata la spaziatura. La dimensione dipende dalla scala di dettaglio e dal livello di precisione dell’analisi, pertanto la sua definizione non è immediata ma è relativa al caso in esame.

Per ciascuna delle n unità territoriali, identificate da un codice alfanumerico, si procede al calcolo di quattro indicatori: rapporto di urbanizzazione, indice di fabbricazione territoriale, prossimità alle reti, prossimità agli attrattori, che divengono i fattori o attributi delle stesse (Tabella 1).

In questo modo si ottengono delle factor map. Una factor map è una mappa che mostra per un dato fattore la posizione geografica e la distribuzione di tipi di fattori, dove per tipi di fattori si intendono le variazioni all’interno di ciascun fattore (ad esempio, i gradi di pendenza se il fattore è la pendenza).

Nella seconda fase si procede alla manipolazione delle factor map precedentemente ottenute attraverso un metodo di combinazione che si fonda sul funzionamento di un sistema inferenziale fuzzy che processa in serie le n unità territoriali in cui è stato suddiviso il territorio restituendo la rappresentazione dei diversi ambiti.

Occorre dunque sviluppare il sistema inferenziale fuzzy il cui funzionamento ricordiamo si compone di tre fasi: la fuzzificazione dell’input, l’inferenza fuzzy e la defazzificazione.

Lo sviluppo comprende le seguenti fasi:

- definizione delle variabili di input e output;

- definizione della funzione di appartenenza;

- definizione delle regole del motore decisionale;

- test del sistema.

Le variabili di input sono gli indicatori ottenuti nella fase precedente e cioè: rapporto di urbanizzazione, indice di fabbricazione territoriale, prossimità alle reti, prossimità agli attrattori. La variabile di output è la suitability, ovvero l’appartenenza ad uno dei cinque ambiti in cui si è pensato di suddividere il territorio.

La definizione delle funzioni di appartenenza comporta la definizione dell’universo del discorso e la definizione della forma e del numero delle funzioni. Per quanto riguarda l’universo del discorso di una variabile essa deve coincidere con l’intervallo dei valori da essa realmente assunti nel contesto del reale funzionamento del sistema, invece per la forma generalmente si scelgono forme semplici.

Per la variabile indice di fabbricazione territoriale, l’universo coincide con un intervallo che va da zero e il max valore che ritroviamo nel caso di studio ed è suddiviso in cinque classi: molto piccolo (MP), piccolo (P), medio (M), grande (G), molto grande (MG) di cui le classi estreme rappresentate da funzioni trapezoidali e quelle intermedie da funzioni triangolari.

Per l’universo della variabile rapporto di urbanizzazione, che coincide con un intervallo compreso tra zero ed uno per la natura adimensionale dell’indicatore, si è adottata una analoga ripartizione con differenti supporti.

Per le restanti due variabili di input, prossimità alle reti e prossimità agli attrattori, l’universo va da zero al max valore registrabile nel caso di studio ed è suddiviso rispettivamente in tre classi: piccolo (P), medio (M), grande (G), la prima; e in due: piccolo (P), grande (G), la seconda, con funzioni ancora trapezoidali e triangolari.

Per la variabile di output l’universo viene suddiviso in cinque classi di uguale ampiezza rappresentate da funzioni triangolari.

Per quanto riguarda la definizione delle regole motore decisionale, vediamo che esse derivano dalle osservazioni, dal comportamento degli operatori e da interviste a esperti del problema in questione.

Ad esempio un sistema con 4 input, ciascuno caratterizzato da 5 funzioni e 3 output richiederebbe un max di 54 x 3 = 1.875 regole. In realtà, il numero di regole è decisamente inferiore e oscilla tra venti e quaranta.

Nella fase di test del sistema si valutano le risposte che esso fornisce nei confronti di una serie di dati di input, e si correggono eventuali anomalie modificando o aggiungendo regole e/o funzioni di appartenenza.

Caso applicativo

La metodologia proposta è stata applicata per analizzare il tessuto insediativo del Comune di Taurasi, in Provincia di Avellino.

Prima fase

Delimitata l’area di studio, che è stata ristretta alla porzione di territorio più significativa rispetto alla analisi che ci accingiamo a fare, si è proceduto alla discretizzazione sovrapponendo ad essa una griglia a maglie quadre di lato 50 metri. Ne è scaturita una suddivisione in 1.326 unità territoriali, ciascuna delle quali è stata identificata con un codice alfanumerico (Figura 2).

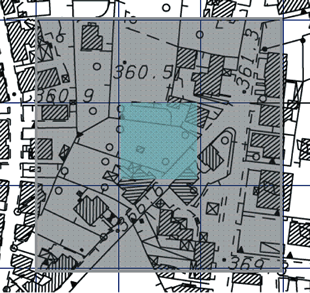
Per ciascuna unità territoriale si è proceduto a calcolare la superficie coperta, intesa come la parte di superficie direttamente occupata da strade, edifici e attrezzature, e la relativa eventuale volumetria. Questo ha consentito di automatizzare il calcolo dei quattro indicatori attraverso un foglio di calcolo. In particolare, per quanto riguarda il calcolo dell’indice di fabbricazione territoriale e del rapporto di urbanizzazione, si è considerata un’area di influenza per ciascuna unità territoriale data da una corona di unità intorno ad essa (Figura 3).

Per il calcolo invece della distanza dalle reti e dagli attrattori si è selezionata la rete stradale a mezzo del suo grafo, e si è scelto come attrattore l’edificio municipale essendo il comune di piccole dimensioni.

Seconda fase

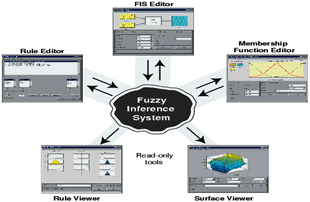
Per lo sviluppo del sistema si è scelto un ambiente informatico specializzato per l’implementazione dei sistemi fuzzy: Matlab fuzzy logic toolbox (Figura 4).

Una volta dichiarate le variabili, che ricordiamo essere per l’input l’indice di fabbricazione territoriale, il rapporto di urbanizzazione, la distanza dalle strade, la distanza dalle centralità, e per l’output la suitability ai diversi ambiti, e definiti per ciascuna di esse il numero e la forma delle funzioni di appartenenza, si procede alla fuzzificazione dei dati ottenendo così delle factor map fuzzificate (Figura 5).

Per quanto riguarda la definizione delle regole, che sono del tipo if-then, si è partiti da quelle più ovvie:

- se l’indice volumetrico è molto grande e il rapporto urbanistico è molto grande e la distanza dalla strada è piccola e la distanza dalla centralità è piccola allora l’ambito territoriale è urbano;

- se l’indice volumetrico è grande e il rapporto urbanistico è grande e la distanza dalla strada è piccola e la distanza dalla centralità è piccola allora l’ambito territoriale è periurbano ad alta densità;

- se l’indice volumetrico è medio e il rapporto urbanistico è medio e la distanza dalla strada è piccola e la distanza dalla centralità è piccola allora l’ambito territoriale è periurbano a bassa densità;

- se l’indice volumetrico è piccolo e il rapporto urbanistico è piccolo e la distanza dalla strada è grande e la distanza dalla centralità è grande allora l’ambito territoriale è metaurbano;

- se l’indice volumetrico è molto piccolo e il rapporto urbanistico è molto piccolo e la distanza dalla strada è grande e la distanza dalla centralità è grande allora l’ambito territoriale è extraurbano;

per giungere, dopo aver analizzato dati e risultati nella fase di tunning, alla individuazioni di ben 20 regole.

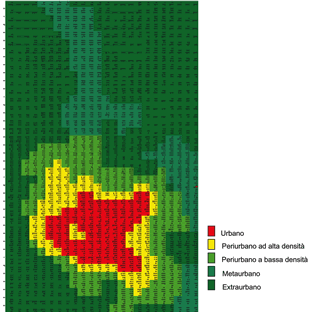
Con questi nuovi cambiamenti si è giunti ad una prima individuazione esaustiva dei 5 ambiti territoriali (Figure 6 e 7).

Considerazioni conclusive

La descrizione dei tessuti insediativi richiede un notevole sforzo interpretativo soprattutto a causa della complessità mostrata dai fenomeni di diffusione e dispersione urbana.

L’approccio descritto nel presente lavoro ha lo scopo di indicare una possibile applicazione dei sistemi inferenziali fuzzy come strumento per individuare i diversi ambiti di cui si compongono i tessuti insediativi, al fine di fornire una base di riferimento oggettiva, basata su criteri predeterminati, che possa limitare l’arbitrarietà delle perimetrazioni. In particolare, un possibile sviluppo dell’applicazione della metodologia proposta, testata sul Comune di Taurasi, è quello di ridurre la dimensione della maglia della griglia e verificare la risposta del sistema, eventualmente ricalibrato, per cercare di raggiungere una definizione più netta dei diversi ambiti.

La tesi di laurea dal titolo “Ipotesi applicativa della logica fuzzy alle problematiche urbanistico-territoriali”, è stata discussa nell’A.A. 2005/2006, relatore Prof. Ing. Roberto Gerundo, correlatrice Ing. Marialiuisa Petti.

Bibliografia

Bruce D., Kishore T. (2003), Landscape visibility modeling using fuzzy logic and geographical information system, The 8th International Conference on Computers in Urban Planning and Urban Management, Sendai, Japan 27-29 May, 2003.

Cammarata S. (1997), Sistemi con logica fuzzy come rendere intelligenti le macchine, Etas Libri, Milano.

Dell’Acqua G., Lamberti R. (2001), Un approccio inferenziale fuzzy per la delimitazione dei corridoi preferenziali per infrastrutture lineari di trasporto, relazione presentata nel corso della seconda Conferenza nazionale su Informatica e pianificazione urbana e territoriale Input 2001, Isole Tremiti.

Faggiani A. (1999), La logica fuzzy nella soluzione dei problemi territoriali multricriteriali, Tesi di laurea Daest, Venezia.

Fregolent L. (2005), Pianificazione e sostenibilità ambientale nella città a bassa densità, Atti Urbing alta formazione, Potenza.

Heikkila E. D., Shen T., Yang K. (2001), Fuzzy urban systems, in “The 7th International Conference on Computers in Urban Planning and Urban Management”, University of Hawaii at Manoa Honolulu, Hawaii USA 18-20 July, 2001.

Murgante B., Sansone A. (2005), L’uso della densità di Kernel e del rough set per la definizione degli ambiti periurbani, Atti Urbing alta formazione, Potenza.

Galioto P., Ardizzone A.(2005), La tecnologia Gis per la perimetrazione e la qualificazione degli agglomerati di edilizia rada in aree extraurbane, in Cecchini A., Plaisant A. (a cura), “Analisi e modelli per la pianificazione Teoria e Pratica: lo stato dell’arte”, FrancoAngeli, Milano.

Zadeh L. A. (1965), Fuzzy Sets, Journal of Information and Control 8.